Решение досрочного ЕГЭ 2015 по математике (март) 11 класс

перейти к условиям задач

14. Материал сайта www.itmathrepetitor.ru Стандартный алгоритм: находим производную функции \(y=33x-30\sin x+29\) и приравниваем к нулю. Среди найденных корней уравнения (это нули производной) выбираем лишь те, которые принадлежат отрезку \([-\pi/2; 0]\). Добавляем к этим корням концевые точки отрезка \(-\pi/2\) и \(0\). А далее подставляем полученные значения в саму функцию \(y=33x-30\sin x+29\) (не в производную!) вместо \(x\) и определяем наибольшее среди получившихся \(y\).
    Это все слова. Давайте конкретнее: \(y’=(33x)’-(30\sin x)’+29’=33-30\cos x\). Для вычисления производной пригодились правила и таблица производных. Из уравнения \(33-30\cos x=0\) следует, что \(\cos x=\displaystyle\frac{11}{10}\). И кто-то от радости, что получилось простейшее уравнение, начинает применять формулу \(x=\pm\arccos\displaystyle\frac{11}{10}+2\pi n, n\in Z\), не обращая внимание на факт \(\displaystyle\frac{11}{10}>1\). Правильный ответ уравнения: корней нет. Поэтому рассматривать будем лишь концевые точки \(-\displaystyle\frac{\pi}{2}\) и \(0\). При \(x=0\) значение функции (не производной!) \(y=33\cdot 0-30\sin 0+29=29\). При \(x=-\displaystyle\frac{\pi}{2}\) значение \(y=33\cdot (-\displaystyle\frac{\pi}{2})-30\sin(-\displaystyle\frac{\pi}{2})+29\)\(=-\displaystyle\frac{33\pi}{2}+59<29\). То есть наибольшее значение равно \(29\).
15. а) Разложим на множители левую часть уравнения методом группировки: \(\cos^2 x\cdot (2\cos x-1)+(2\cos x-1)=9\)\(\Leftrightarrow (2\cos x -1)(\cos^2 x+1)=0\). Произведение равно нулю, значит, хотя бы один из множителей равен нулю. То есть \(2\cos x-1=0\) или \(\cos^2 x+1=0\). Второе уравнение не имеет корней, так как единица плюс неотрицательное число всегда больше нуля. Из первого уравнения получаем, что \(\cos x=\displaystyle\frac{1}{2}\Leftrightarrow x=\pm\displaystyle\frac{\pi}{3}+2\pi n, n\in Z\).
    б) Разобьем формулу \(x=\pm\displaystyle\frac{\pi}{3}+2\pi n, n\in Z\) на две более простых: 1)\(x=\displaystyle\frac{\pi}{3}+2\pi n, n\in Z\); 2) \(x=-\displaystyle\frac{\pi}{3}+2\pi n, n\in Z\). Найдем корни из первой формулы, которые принадлежат \([2\pi; \frac{7\pi}{2}]\). Для этого решим двойное неравенство \(2\pi\le \displaystyle\frac{\pi}{3}+2\pi n\le \displaystyle\frac{7\pi}{2}\) \(\Leftrightarrow 12\le 2+12n\le 21\) (после сокращения на \(\pi\) и избавления от знаменателя)\(\Leftrightarrow \displaystyle\frac{5}{6}\le n\le \displaystyle\frac{19}{12}\). Так как \(n\in Z\), то есть по-русски \(n\) – целое число (что это такое, смотрите здесь), то \(n=1\). Тогда после подстановки в первую формулу получаем угол \(\displaystyle\frac{\pi}{3}+2\pi=\displaystyle\frac{7\pi}{3}\).
    Аналогично поступаем со второй формулой: \(2\pi\le -\displaystyle\frac{\pi}{3}+2\pi n\le \displaystyle\frac{7\pi}{2}\)\(\Leftrightarrow \displaystyle\frac{7}{6}\le n\le \displaystyle\frac{23}{12}\). Данному неравенству никакое целое \(n\) не удовлетворяет. Значит, итоговый ответ пункта б): \(\displaystyle\frac{7\pi}{3}\).
16. Проведем прямую через точку \(K\) параллельно \(BD_1\) до пересечения с прямой \(B_1D_1\) в точке \(F\) (смотрите рисунок). Точка \(F\) существует, так как точки \(K, B, D_1\) и \(B_1\) лежат в одной плоскости. Через точки \(F\) и \(C_1\) проведем прямую до пересечения с ребром \(A_1B_1\) в некоторой точке. Именно в этой точке плоскость \(\alpha\) пересекает ребро \(A_1B_1\), то есть это точка \(P\) .  Треугольники \(KB_1F\) и \(BB_1D_1\) подобны, значит, \(B_1F:FD_1 = 2:3\). Рассмотрим на плоскости грань \(A_1B_1C_1D_1\) (смотрите второй рисунок).
    Продлим \(C_1P\) до пересечения с продолжением \(A_1D_1\) в точке \(T\). Треугольники \(TFD_1\) и \(FB_1C_1\) подобны, значит, \(B_1F:FD_1=B_1C_1:TD_1\), то есть \(2:3=5:TD_1\), откуда \(TD_1=\displaystyle\frac{5}{2}\). Тогда \(TA_1=\displaystyle\frac{5}{2}-5=\displaystyle\frac{5}{2}\). Осталось заметить подобие треугольников \(TPA_1\) и \(PB_1C_1\), из которого следует, что \(A_1P:PB_1=TA_1:B_1C_1\), то есть \(A_1P:PB_1=1:2\).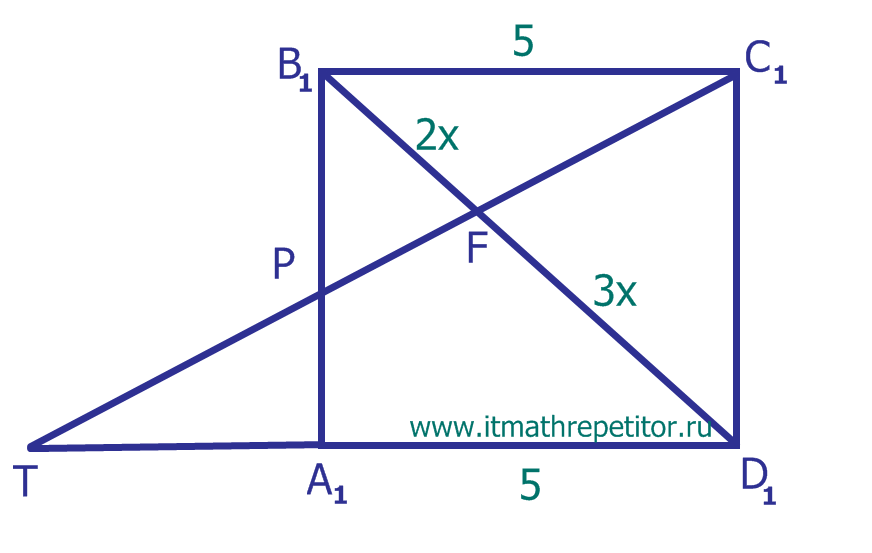 
    б) Объем большей части найдем как разность объема куба и меньшей части. Объем куба равен 125. Меньшая часть является треугольной пирамидой \(KPB_1C_1\), объем которой можно найти по формуле \(\displaystyle\frac{1}{3}S_{KB_1P}\cdot B_1C_1\). Известно из условия, что \(B_1C_1\) равно 5, \(B_1K\) равно 2,  а из пункта а), что \(PB_1\) равно \(\displaystyle\frac{10}{3}\). Тогда искомый объем равен \(125-\displaystyle\frac{1}{3}\cdot 5\cdot\frac{2\cdot \frac{10}{3}}{2} = \frac{1075}{9}\).
17. Материал сайта www.itmathrepetitor.ru Сразу заметим, что \(\log_{0,5}(4+3x-x^2)=-\log_2(4+3x-x^2)\). Тогда после замены \(t=\log_2(4+3x-x^2)\) неравенство принимает вид \(t^2-7t+10>0\). Данное неравенство можно решить методом интервалов, для этого разложим левую часть на множители \((t-5)(t-2)>0\). Конечно, стоит научиться решать квадратные неравенства почти устно. В общем, \(t\in (-\infty; 2)\cup (5; +\infty)\). Вернемся к переменной \(x\) и запишем данный ответ в виде совокупности двух неравенств \(\log_2(4+3x-x^2)>5\) и \(\log_2(4+3x-x^2)<2\).
    Рассмотрим первое неравенство. Так как \(5=\log_2{32}\), то оно равносильно неравенству \(4+3x-x^2>32\Leftrightarrow x^2-3x+28<0\). Данное неравенство не имеет решений, так как квадратный трехчлен не имеет корней и коэффициент при \(x^2\) больше нуля (то есть квадратный трехчлен принимает только положительные значения).
    Рассмотрим второе неравенство. Оно равносильно системе неравенств \(\left\{\begin{array}{l l} 4+3x-x^2<4,\\ 4+3x-x^2>0\end{array}\right.\) \(\Leftrightarrow \left\{\begin{array}{l l} x(x-3)>0,\\ (x-4)(x+1)<0\end{array}\right.\) \(\Leftrightarrow \left\{\begin{array}{l l} x\in (-\infty; 0)\cup (3;+\infty),\\ x\in (-1;4)\end{array}\right.\). Тогда \(x\in(-1;0)\cup (3;4)\).
18. а) Пусть точки \(T\) и \(R\) – точки касания окружности со сторонами \(AB\) и \(AD\) соответственно. Точка \(F\) – точка касания окружности с прямой \(MN\). По свойству касательных, проведенных из одной точки к окружности, \(TM = MF\), \(FN = NR\) и \(AT=AR\). Тогда \(P_{MAN}=MA+MF+FN+AN=MA+TM+NR+AN=TA+AR\)\(=2TA\). Но \(TA\) равно половине стороны квадрата. Значит, \(P_{MAN}\) равен стороне квадрата.

смотрите еще Репетиционный вариант ЕГЭ март, 2015