ЕГЭ Пробный вариант по математике 11 класс 2014

Профильный уровень

Вариант 6

Условия задач с ответами и решениями

Часть 1

1. Магазин делает пенсионерам скидку 5 %. Пенсионер заплатил за десяток яиц в этом магазине 33 рубля 25 копеек. Сколько рублей стоит в этом магазине десяток яиц без скидки? Решение

2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 15 октября. Ответ дайте в градусах Цельсия. Решение

3.  Из пункта А в пункт D ведут три дороги. Одновременно из А в D выехали грузовик, автобус и легковой автомобиль. Грузовик едет через пункт В со средней скоростью 58 км/ч, автобус едет через пункт С со средней скоростью 48 км/ч. По третьей дороге – без промежуточных пунктов – едет легковой автомобиль со средней скоростью 52 км/ч. На рисунке показана схема дорог и расстояние (в км) между пунктами по дорогам. Какое транспортное средство доберется до D позже других? В ответе укажите, сколько часов оно будет находиться в пути. Решение

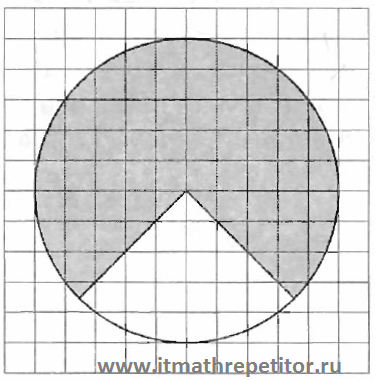
4.  На клетчатой бумаге изображен круг. Какова площадь круга, если площадь заштрихованного сектора равна 45? Решение

5. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 6, но не дойдя до отметки 12.  Решение

6. Найдите корень уравнения \(x^2-15=(x+1)^2\). Решение

7. В треугольнике ABC угол АСВ равен 90 градусов, АВ равно 5, АС равно \(\sqrt{21}\). Найдите косинус угла АВС. Решение

8. На рисунке изображен график некоторой функции \(y=f(x)\) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите \(F(7)-F(3)\), где \(F(x)\) – одна из первообразных функции \(y=f(x)\). Решение

9. Площадь полной поверхности конуса равна 24. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса. Решение

Часть 2

10. Найдите значение выражения \(8\cdot\sqrt[5]{16}\cdot\sqrt[20]{16}\) Решение

11. Трактор тащит сани с силой \(F=80\) кН, направленной под острым углом \(\alpha\) к горизонту. Работа трактора (в килоджоулях) на участке длиной \(S=90\) м вычисляется по формуле \(A=FS\cos\alpha\). При каком максимальном угле \(\alpha\) (в градусах) совершенная работа будет не менее 3600 кДж? Решение

12. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60 градусов. Высота пирамиды равна 18. Найдите объем пирамиды.

13. Первые 110 км автомобиль ехал со скоростью 60 км/ч, следующие 100 км – со скоростью 90 км/ч, а затем 150 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. Решение

14. Найдите наибольшее значение функции \(y=\log_3(-7+8x-x^2)+8\) Решение

15. Дано уравнение \(ctg^2 x+2\sqrt{3} ctg x+3\sin^2 x=-3\sin^2 (x-\frac{3\pi}{2})\) а) Решите уравнение б) Найдите все решения уравнения на отрезке \([-\frac{11\pi}{2}; -4\pi]\). Решение

16. На ребре \(AA_1\) куба \(ABCDA_1B_1C_1D_1\) отмечена точка \(K\) так, что \(AK=6\) и \(KA_1=2\). Точка \(O\) – центра грани \(ABCD\) куба. а) Постройте сечение куба плоскостью \(D_1OK\). б) Найдите объем меньшей из частей куба, на которые он разбивается указанной плоскостью.

17. Решите неравенство \(\log_{4x+5x^2}5-\log_{4x}5\le 0\)

18. На сторонах \(AD\) и \(BC\) параллелограмма \(ABCD\) взяты соответственно точки \(M\) и \(N\), причем \(M\) – середина \(AD\), а \(BN : NC = 1 : 3\). а) Докажите, что прямые \(AN\) и \(AC\) делят отрезок \(BM\) на три равные части б) Найдите площадь четырехугольника, образованного пересечениями прямых \(AN\), \(AC\), \(BD\) и \(BC\), если площадь параллелограмма \(ABCD\) равна 30.

19. 31 декабря 2013 года Сергей взял в банке кредит под 10% годовых. Схема выплаты кредита следующая – 31 декабря каждого последующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк 53 240 рублей. Сергей выплатил долг тремя равными платежами. Какова сумма, взятая Сергеем в долг?

20. Найдите все значения параметра \(a\), при каждом из которых система уравнений \(\left\{\begin{array}{l l} 6x^2+6y^2=13xy ,\\ (x-3a)^2+(y-3a)^2=13a^4\end{array}\right.\) имеет ровно два решения.

21. Из 26 последовательных нечетных чисел 1, 3, 5, …, 51 выбрали 11 различных чисел, которые записали в порядке возрастания. Пусть \(A\) – шестое по величине среди этих чисел, а \(B\) – среднее арифметическое выбранных одиннадцати чисел. а) Может ли \(B-A\) равняться \(\frac{3}{11}\)? б) Может ли \(B-A\) равняться \(\frac{4}{11}\)? в) Найдите наибольшее возможное значение \(B-A\).

смотрите еще Досрочный ЕГЭ (март, 2015) по математике

и Репетиционный вариант ЕГЭ (март, 2015) по математике

Ответы

1. 35 руб
2. 5
3. легковой, 2,25 ч
4. 60
5. 0,5
6. -8
7. 0,4
8. 7,5
9. 6
10. 16
11. 60
12. 1296\(\sqrt{3}\)
13. 81
14. 10
15. а) \(-\frac{\pi}{6}+\pi n, n\in Z\) б) \(-\frac{25\pi}{6}; -\frac{31\pi}{6}\)
16. б) \(\frac{2368}{21}\)
17. \((0; \frac{1}{5})\cup (\frac{1}{4}; +\infty)\)
18. скоро
19. 132400
20. скоро
21. скоро