ЕГЭ 2014 Типовой вариант 6
Условия задач с ответами и решениями

B1. В летнем лагере на каждого участника полагается 30 г сахара в день. В лагере 223 человека. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 8 дней?

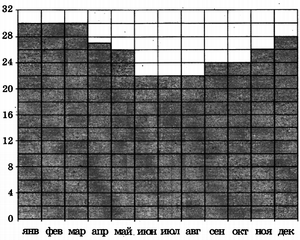
B2. На диаграмме показана среднемесячная температура воздуха в Рио-де-Жанейро за каждый месяц 2009 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячной температурой в 2009 году. Ответ дайте в градусах Цельсия.

B3. Найдите площадь трапеции, вершинами которой являются точки с координатами (1;6), (7;6), (4;1), (2;1).

B4. В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трех городах России (по данным на начало 2010 года). Определите, в каком из этих городов окажется самым дешевым следующий набор продуктов: 2 батона пшеничного хлеба, 3 кг говядины, 1 л подсолнечного масла. В ответ запишите стоимость данного набора продуктов в этом городе (в рублях)

B5. Найдите корень уравнение$\displaystyle (\frac{1}{36})^{x-2}=6$

B6. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 11, а одна из диагоналей ромба равна 44. Найдите величину тупого угла ромба. Ответ дайте в градусах.

B7. Найдите значение выражения $\displaystyle (558^2-23^2):581$.

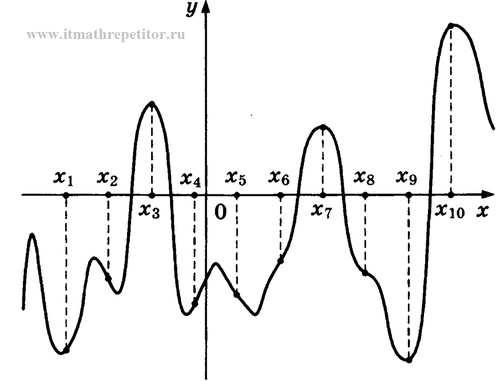
B8. На рисунке изображен график функции $y=f(x)$  и десять точек на оси абсцисс: $x_1,x_2,x_3,\ldots,x_{10}$. В скольких из этих точек производная $f'(x)$ функции $f(x)$ положительна?

B9. Высота правильной четырехугольной пирамиды равна 12, а сторона основания равна 8. Найдите тангенс угла между плоскостью боковой грани и плоскостью основания пирамиды.

B10. В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,4. Вероятность того, что чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.

B11. Стороны основания правильной четырехугольной пирамиды равна 6, боковые ребра равны 5. найдите площадь поверхности этой пирамиды.

B12. Для обогрева помещения температура в котором равна T_п = 20^о С, через радиатор отопления пропускают горячую воду температурой Т_в = 88^о С. Расход проходящей через трубу воды m = 0,4 кг/c. Проходя по трубе расстояние x (м), вода охлаждается до температуры T (^oC), причем $x=\displaystyle \alpha\frac{cm}{\gamma}\log_2\frac{T_B-T_n}{T-T_n}$ (м), где с = 4200 Дж/(кг$\cdot$^oC) - теплоемкость воды, $\gamma = 63$ Вт/(м$\cdot$^oC) - коэффициент теплообмена, $\alpha = 1,2$ - постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы равна 64 м?

B13. В четверг акции компании подорожали на некоторое число процентов, а в пятницу подешевели на то же число процентов. В результате они стали стоить на 9% дешевле, чем при открытие торгов в четверг. На сколько процентов подорожали акции компании в четверг?

B14. Найдите наибольшее значение функции $y=-\frac{2}{3}x\sqrt{x}+3x+19$ на отрезке $[8; 21]$

С1. а) Решите уравнение $\displaystyle 6\sin^2 x+7\cos x-7=0$ б) Найдите все корни этого уравнения, принадлежащие отрезку $[-3\pi; -\pi]$.

С2. В правильной треугольной призме ABCA₁B₁C₁ ребро основания AB = $8\sqrt{3}$, а боковое ребро АА₁ = 7. Найдите тангенс угла между плоскостями BCA₁ и BB₁C₁.

С3. Решите  систему неравенств $\left\{\begin{array}{l l} \log_7^2(x^2+4x-20)\leq x-3,\\ \displaystyle \log_7^2(x^2+2x-14)\leq 3-x \end{array}\right.$

С4. Дан параллелограмм со сторонами 1 и 2 и острым углом 60^о. На двух его несмежных сторонах как на основаниях построены вне параллелограмма равнобедренные треугольники с углами 120^о при вершинах. Найдите расстояние между этими вершинами.

С5. Найдите все значения параметра $a$, при каждом из которых  уравнение $\displaystyle |\log_{0,5}(x^2)-a|-|\log_{0,5}x+2a|=(\log_{0,5}x)^2$ имеет хотя бы одно решение, меньшее 2.

С6. Друг за другом подряд выписали десятичную запись чисел $2^{50}$ и $5^{50}$. Сколько всего цифр выписали?

Ответы

B1. 54
B2. 8
B3. 20
B4. 786
B5. 1,5
B6. 120
B7. 535
B8. 3
B9. 3
B10. 0,4
B11. 84
B12. 37
B13. 30
B14. 28
C1. а) $2n\pi, \pm arccos(1/6)+2m\pi, n,m\in Z$ б)$-2\pi-arccos(1/6), -2\pi+arccos(1/6)$
C2. $12/7$
C3. $3$
C4. $\displaystyle \sqrt{\frac{13}{3}}$ или $\displaystyle\sqrt{\frac{19}{3}}$
C5. $-9/4< a<2$
C6. 51