ЕГЭ 2014 Типовой вариант 5
Условия задач с ответами и решениями

B1. Больному прописан курс лекарств, которое нужно пить по 0,5 г три раза в день в течение трех недель. В одной упаковке содержится 10 таблеток по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс?

B2. На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8-го класса по математике в 2007 году (по 1000-балльной шкале). Среди указанных стран третье место принадлежит Австралии. Определите, какое место занимает Тунис.

B3. Площадь треугольника АВС равна 28. DE – средняя линия. Найдите площадь трапеции ABDE.

B4. Трое решают, как им обойдется дешевле доехать из Москвы в Санкт-Петербург – на поезде или в автомобиле. Билет на поезд стоит 600 рублей на одного человек. Автомобиль расходует 10 литров бензина на 100 километров пути, расстояние по шоссе равно 700 километров, а цена бензина равна 19 рублям за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?

B5. Найдите корень уравнение\(\log_{1/5}(5-x)=-2\)

B6. Один острый угол прямоугольного треугольника на 30^о больше другого. Найдите больший острый угол.

B7. Найдите значение выражения \(\displaystyle\frac{18}{3^{\log_32}}\).

B8. На рисунке изображен график первообразной функции \(y=F(x)\) некоторой функции \(y=f(x)\), определенной на интервале (-16; -2). Пользуясь рисунком, определите количество решений уравнения \(f(x)=0\) на отрезке [-15; -8]

B9. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке О. Площадь треугольника ABC равна 16, объем пирамиды равен 80. Найдите длину отрезка OS.

B10. Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку G.

B11. Объем данного правильного тетраэдра равен 3 см³. Найдите объем правильного тетраэдра, ребро которого в 4 раза больше ребра данного тетраэдра. Ответ дайте в см³.

B12. Компания Яндекс-Маркет вычисляет рейтинг интернет-магазинов по формуле, указанной на рисунке, где r_пок –  средняя оценка магазина покупателями (от 0 до 1), r_экс – оценка магазина экспертами компании (от 0 до 0,7) и К – число покупателей, оценивших магазин. Найдите рейтинг интернет магазина “Эпсилон” , если число покупателей, оставивших отзыв о магазине, равна 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,61.

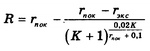
B13. Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 90 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5 часов 24 минуты позже автомобилиста. Ответ дайте в км/ч

B14. Найдите наибольшее значение функции \(y=x^3-18x^2+81x+73\) на отрезке \([0; 7]\)

С1. а) Решите уравнение \(\displaystyle 7^{x^2-2x}+7^{x^2-2x-1}=56\) б) Найдите все корни этого уравнения, принадлежащие отрезку \([-1; 1]\).

С2. В правильной шестиугольной пирамиде SA…F, боковые ребра которой равны 2,  а стороны основания – 1, найдите косинус угла между прямой АС и плоскостью SAF.

С3. Решите  систему неравенств \(\left\{\begin{array}{l l} \log_{x^3-9x^2+27x-27}(9-x)\geq 0,\\ \displaystyle\frac{2}{x^2-12x+35}+\frac{3}{x^2-17x+70}\leq 0\end{array}\right.\)

С4. Окружности с центрами О₁ и О₂ пересекаются в точках А и В. Известно, что угол AO₁B равен 90^о, угол АО₂В равен 60^о, О₁О₂ = a. Найдите радиусы окружностей.

С5. Найдите все значения параметра \(k\), при каждом из которых  уравнение \(\displaystyle\frac{2(k+1)\cos t-k}{\sin t+\cos t}=2\) имеет хотя бы одно решение на отрезке \([\pi/2; \pi ]\).

С6. Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 15 раз больше, либо в 15 раз меньше предыдущего. Сумма всех членов последовательности равна 3825. а) Может ли последовательность состоять из двух членов? б) Может ли последовательность состоять из трех членов? в) Какое наибольшее количество членов может быть в последовательности?

Ответы

B1. 7
B2. 9
B3. 21
B4. 1330
B5. -20
B6. 60
B7. 9
B8. 2
B9. 15
B10. 0,25
B11. 192
B12. 0,81
B13. 10
B14. 181
C1. а) \(1\pm\sqrt{3}\) б)\(1-\sqrt{3}\)
C2. \(\sqrt{5}/5\)
C3. \((5;7); (7;8]\)
C4. \(\displaystyle\frac{a\sqrt{2}}{\sqrt{3}+1}, \frac{2a}{\sqrt{3}+1}\) или \(\displaystyle\frac{a\sqrt{2}}{\sqrt{3}-1},\frac{2a}{\sqrt{3}-1}\)
C5. \( -2\leq k<\sqrt{2}-1\)  или  \(\sqrt{2}-2<k\leq 0\)
C6. а) нет б) да (225, 3375, 225) в) 479