ЕГЭ 2014 Типовой вариант 3
Условия задач с ответами и решениями

B1. Сырок стоит 5 руб 40 коп. Какое наибольшее число сырков можно купить на 40 рублей?

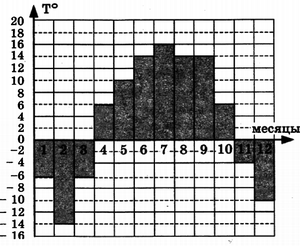
B2. На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1994 году. Ответ дайте в градусах Цельсия.

B3. Найдите площадь квадрата ABCD. Размер каждой клетки  1 см х 1 см. Ответ дайте в квадратных сантиметрах.

B4. В магазине одежды объявлена акция - если покупатель приобретет товар на сумму свыше 5000 руб., он получает скидку на следующую покупку в размере 10%. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель В. хочет приобрести куртку ценой 4500 руб., рубашку ценой 800 руб. и кеды ценой 1600 руб. В каком случае В. заплатит за покупку меньше всего?

1. В. купит все три товара сразу.

2. В. купит сначала куртку и рубашку, а потом кеды со скидкой.

3. В. купит сначала куртку и кеды, а потом рубашку со скидкой.

В ответ запишите сумму, которую заплатит В. за покупку в этом случае.

B5. Найдите корень уравнения $5^{4-x}=25$

B6. Найдите вписанный угол, опирающийся на дугу, которая составляет 1/5 окружности.

B7. Найдите значение выражения $\displaystyle\frac{5\sin 61^o}{\sin 299^o}$.

B8. На рисунке изображен график функции $y=f(x)$ и касательная к этому графику, проведенная в точке $x_o$. Уравнение касательной показано на рисунке. Найдите значение производной функции $y=-\frac{1}{4}f(x)+5$ в точке $x_o$

B9. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 30^о. Боковое ребро равно 3. Найдите диагональ призмы.

B10. В среднем на 150 карманных фонариков приходится три неисправных. Найдите вероятность купить работающий фонарик.

B11. В цилиндрический сосуд, в котором находится 4 литра воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.

B12. В электросеть включен предохранитель, рассчитанный на силу тока 16 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Сила тока в цепи I связана с напряжением U соотношением $I=\displaystyle\frac{U}{R}$, где R - сопротивление электроприбора. Ответ выразите в омах.

B13. Моторная лодка прошла против течения 24 км и вернулась обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите скорость (в км/ч) лодки в неподвижной воде, если скорость течения равна 3 км/ч.

B14. Найдите наименьшее значение функции $y=5\cos x-6x+4$ на отрезке $[-3\pi/2; 0]$

С1. а) Решите уравнение $\displaystyle (49^{\cos x})^{\sin x}=7^{\sqrt{2}\cos x}$ б) Найдите все корни этого уравнения, принадлежащие отрезку $[5\pi/2; 4\pi]$.

С2. В правильной треугольной пирамиде SABC с вершиной S, все ребра которой равны 4, точка N - середина ребра АС, точка О - центр основания пирамиды, точка Р делит отрезок SO в отношении 3:1, считая от вершины пирамиды. Найдите расстояние от точки В до прямой NP.

С3. Решите  систему неравенств

С4. Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров. а) Докажите, что периметр треугольника с вершинами в центрах трех окружностей равен диаметру наибольшей из этих окружностей. б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2.

С5. Найдите все значения параметра $a$, при каждом из которых модуль уравнение имеет хотя бы одно решение.

С6. Найдутся ли хотя бы три десятизначных числа, делящихся на 11, в записи каждого из которых использованы все цифры от 0 до 9?

Ответы

B1. 7
B2. 30
B3. 5
B4. 6740
B5. 2
B6. 36
B7. -5
B8. 0,5
B9. 6
B10. 0,98
B11. 2
B12. 13,75
B13. 21
B14. 9
C1. а) $\pi/2+\pi k, \pi/4+2\pi k, 3\pi/4+2\pi k, k\in Z$ б)$5\pi/2; 11\pi/4; 7\pi/2$
C2. 2
C3. $[2;+\infty)$
C4. 3
C5. $(-\infty;0]; (2+\sqrt{2};+\infty)$
C6. да