ЕГЭ 2014 Типовой вариант 2
Условия задач с ответами и решениями

B1. Пакет молока стоит 40 рублей. Пенсионерам магазин делает скидку 15%. Сколько рублей заплатит пенсионер за пакет молока?

B2. На диаграмме показана среднемесячная температура воздуха (в градусах Цельсия) в Хабаровске по результатам многолетних наблюдений. Найдите по диаграмме количество месяцев, когда среднемесячная температура в Хабаровске отрицательна.

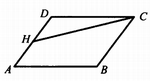
B3. Площадь параллелограмма АВСD равна 3. Точка H - середина стороны AD. Найдите площадь трапеции AHCB.

B4. Для того, чтобы связать свитер, хозяйке нужно 400 граммов шерстяной пряжи красного цвета. Можно купить красную пряжу по цене 60 рублей за 50 граммов, а можно купить неокрашенную пряжу по цене 50 рублей за 50 граммов и окрасить ее. Один пакетик краски стоит 10 рублей и рассчитан на окраску 200 граммов пряжи. Какой вариант покупки дешевле? В ответ напишите, сколько рублей будет стоить эта покупка.

B5. Найдите корень уравнения $(x+7)^3=216$

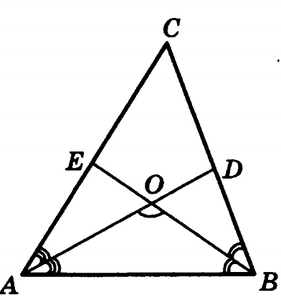
B6. В треугольнике ABC угол С равен 58^о, биссектрисы AD и BE пересекаются в точке О. Найдите угол АОВ. Ответ дайте в градусах.

B7. Найдите $\cos\alpha$, если$\sin\alpha=\frac{\sqrt{21}}{5}$ и $\alpha\in (\pi/2; \pi)$.

B8. На рисунке изображен график $y=F(x)$ одной из первообразных некоторой функции $f(x)$, определенной на интервале (-8; 7). Пользуясь рисунком, определите количество решений уравнения $f(x)=0$ на отрезке [-5; 5].

B9. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все ребра которой равны 5, найдите угол между прямыми FA и D₁E₁. Ответ дайте в градусах.

B10. В среднем из 900 садовых насосов, поступивших в продажу, 27 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

B11. В сосуде, имеющем форму конуса, уровень жидкости достигает $\frac{1}{2}$ высоты. Объем жидкости равен 25 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

B12. Емкость высоковольтного конденсатора в телевизоре $C = 4\cdot 10^{-6}$ Ф. Параллельно с конденсатором подключен резистор с сопротивлением $R = 2\cdot 10^6$ Ом. Во время работы телевизора напряжение на конденсаторе $U_o=22$ кВ. После выключения телевизора напряжение на конденсаторе убывает до значения $U$ (кВ) за время, определяемое соотношением $t=\alpha RC\log_2\frac{U_o}{U}$ (с), где $\alpha =1,7$ - постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 27,2 секунды. Ответ дайте в кВ (киловольтах).

B13. На изготовление 540 деталей первый рабочий затрачивает на 12 часов меньше, чем второй рабочий на изготовление 600 деталей. Известно, что первый рабочий за час делает на 10 деталей больше, чем второй. Сколько деталей в час делает первый рабочий?

B14. Найдите наибольшее значение функции $y=11\ln (x+4)-11x-5$ на отрезке $[-3,5; 0]$

С1. Решите уравнение $6\sin^2 x-5\sin x-4=0$ и найдите все корни этого уравнения, принадлежащие отрезку $[-7\pi/2; -3\pi/2]$.

С2. В правильной четырехугольной пирамиде SABCD с вершиной S сторона основания равна 8. Точка L - середина ребра SC. Тангенс угла между прямыми BL и SA равен $2\sqrt{\frac{2}{5}}$. Найдите площадь поверхности пирамиды.

С3. Решите неравенство $\log_{\displaystyle\frac{25-x^2}{16}}\frac{24+2x-x^2}{14}>1$.

С4. Окружность, построенная на стороне AC треугольника ABC как на диаметре, проходит через середину стороны ВС и пересекает в точке D продолжение стороны АВ за точку А, причем AD = $\frac{2}{3}$АВ. Найдите площадь треугольника ABC, если AC = 1.

С5. Найдите все значения параметра $a$, при каждом из которых модуль разности корней уравнения $x^2-6x+12+a^2-4a=0$ принимает наибольшее значение.

С6. Известно, что при любом целом $K\ne 27$ число $a-K^3$ делится без остатка на $27-K$. Найдите $a$

Ответы

B1. 34
B2. 5
B3. 2,25
B4. 420
B5. -1
B6. 119
B7. -0,4
B8. 4
B9. 60
B10. 0,97
B11. 175
B12. 5,5
B13. 30
B14. 28
C1. $(-1)^{n+1}\pi/6+\pi n, n\in Z$;  $-17\pi/6, -13\pi/6$
C2. 192
C3. (-4;-3)U(-1;3)
C4. $\sqrt{6}/5$
C5. a=2
C6. a=273