Демонстрационный вариант ГИА (ОГЭ) по математике
10 ноября 2014 года
Часть 1
Модуль “Алгебра”
1. Найдите значение выражения \(\displaystyle\frac{1}{4}+0,07\) Решение
2. На координатной прямой отмечена точка А. Известно, что она соответствует одному из четырех указанных ниже чисел. Какому из чисел соответствует точка А? Решение

1) \(\frac{181}{16}\) 2) \(\sqrt{37}\) 3) \(0,6\) 4) \(4\)
3. Значение какого из выражений является рациональным числом? Решение
1) \(\sqrt{6}-3\) 2) \(\sqrt{3}\cdot\sqrt{5}\) 3) \((\sqrt{5})^2\) 4) \((\sqrt{6}-3)^2\)
4. Решите уравнение \(7x-9=40\) Решение
5. Установите соответствие между графиками функций и формулами, которые их задают. Решение


6. В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число. Решение
7. Найдите значение выражения \(9b+\displaystyle\frac{5a-9b^2}{b}\) при \(a=9\) и \(b=36\) Решение
8.Решение

Модуль “Геометрия”
9. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123o . Найдите величину угла ВАС. Ответ дайте в градусах. Решение

10. Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см. Решение
11. Найдите площадь трапеции, изображённой на рисунке. Решение

12. Найдите тангенс угла AOB треугольника, изображённого на рисунке. Решение

13. Укажите номера верных утверждений. Решение
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует
3) Если в ромбе один из углов равен 90o , то такой ромб — квадрат.
4) В любом параллелограмме диагонали равны.
Модуль “Реальная математика”
14. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.

Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?
1) Отлично 3) Удовлетворительно
2) Хорошо 4) Норматив не выполнен
15. На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в километрах) давление составит 540 миллиметров ртутного столба?

16. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников? Решение
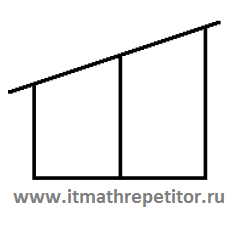
17. Наклонная балка поддерживается тремя столбами, стоящими вертикально на равном расстоянии друг от друга. Длины двух меньших столбов — 60 см и 90 см. Найдите длину большего столба. Ответ дайте в см. Решение
18. Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме.
 Какие из утверждений относительно результатов контрольной работы верны, если всего в школе 120 девятиклассников? В ответе укажите номера верных утверждений.
Какие из утверждений относительно результатов контрольной работы верны, если всего в школе 120 девятиклассников? В ответе укажите номера верных утверждений.
1) Более половины учащихся получили отметку «3».
2) Около половины учащихся отсутствовали на контрольной работе или получили отметку «2».
3) Отметку «4» или «5» получила примерно шестая часть учащихся.
4) Отметку «3», «4» или «5» получили более 100 учащихся.
19. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками. Решение
20. Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле \(T = 2\sqrt{l}\) , где \(l\) — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды. Решение
Часть 2
Модуль “Алгебра”
21. Сократите дробь \(\displaystyle\frac{18^{n+3}}{3^{2n+5}\cdot 2^{n-2}}\) Решение
22. Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч? Решение
23. Постройте график функции \(y=\displaystyle\frac{x^4-13x^2+36}{(x-3)(x+2)}\) и определите, при каких значениях \(c\) прямая \(y = c\) имеет с графиком ровно одну общую точку. Решение
Модуль “Геометрия”
24. В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6 , BC = 8 . Найдите медиану CK этого треугольника. Решение
25. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник. Решение
26. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC. Решение
смотрите еще Типовой вариант 1 ОГЭ 2015 по математике
Ответы
1. 0,32
2. 2
3. 3
4. 7
5. 132
6. 62
7. 1,25
8. 2
9. 57
10. 24
11. 168
12. 2
13. 13; 31
14. 2
15. 2,5
16. 1980
17. 120
18. 13; 31
19. 0,2
20. 2,25
21. 96
22. 8
23. -6,25; -4; 6
24. 5
26. 4,5