Справочник по математике
Числовые ряды
Необходимое условие сходимости ряда

Признаки сходимости для положительных рядов
Признак сравнения
Если  для любого
для любого 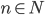 , то из сходимости ряда
, то из сходимости ряда  следует сходимость ряда
следует сходимость ряда  , а из расходимости ряда
, а из расходимости ряда  следует расходимость ряда
следует расходимость ряда 
Предельный признак сравнения
Если  , то при
, то при  ряды
ряды  и
и  или оба сходятся, или оба расходятся. При
или оба сходятся, или оба расходятся. При  из сходимости ряда
из сходимости ряда  следует сходимость ряда
следует сходимость ряда  . При
. При  из расходимости ряда
из расходимости ряда  следует расходимость ряда
следует расходимость ряда 
Степенной признак
Если  при
при 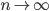 ,
,  , то при
, то при  ряд
ряд  сходится, при
сходится, при  ряд расходится
ряд расходится
Признак Даламбера
Если  , то при
, то при  ряд
ряд  сходится, при
сходится, при 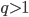 расходится
расходится
Признак Коши
Если ![\displaystyle\lim_{n\to\infty}\sqrt[n]{a_n}=q](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_909fdd86280eb7827e5c48769f21a60f.gif) , то при
, то при  ряд
ряд  сходится, при
сходится, при 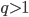 расходится
расходится
Признак Раабе
Если  , то при
, то при 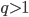 ряд
ряд  сходится, при
сходится, при  расходится
расходится
Интегральный признак
Если функция 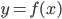 убывает на
убывает на 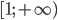 и неотрицательна, то ряд
и неотрицательна, то ряд  сходится или расходится вместе с интегралом
сходится или расходится вместе с интегралом 
Признаки сходимости знакопеременных рядов
Признак Лейбница
Ряд  , где
, где  , сходится, если
, сходится, если 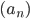 монотонно стремится к нулю
монотонно стремится к нулю
Признак Абеля
Если 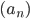 монотонна и ограничена, а ряд
монотонна и ограничена, а ряд  сходится, то сходится ряд
сходится, то сходится ряд 
Признак Дирихле
Если 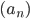 монотонно стремится к нулю, а частные суммы ряда
монотонно стремится к нулю, а частные суммы ряда  ограничены, то ряд
ограничены, то ряд  сходится
сходится